منطق و کنترل فازی

چرا منطق ؟

چون پایه و اساسش همون منطق بولی هست که همه کمابیش با اون آشنا هستن.

چرا فازی؟

منطق بولی فقط دو حالت داشت : 0 و 1 یا بطور روشن تر، سیاه و سفید.

منطق فازی n حالت داره از همین 0 و 1 یا سیاه و سفید ( توجه کنید نمیگم n حالت بین 0 و 1).

مثلا “این رنگ خیلی مایل به سفیده” یعنی این رنگ همچنان همون سفیده اما به میزان مثلا 0.9 (یه ذره تیره تر)

یا یه خورده فازی تر بخوام بگم  “عدد 0.75 خیلی نزدیک به 1 هست” یعنی عدد 0.75 همون 1 هست اما به اندازه 0.75 !!!!!!

 شاید فکر کنید ما داریم لقمه رو دور سرمون میچرخونیم اما این یه تدبیر هوشمندانه از دانشمندان ( مخصوصا پروفسور خودمون) بود که بار محاسبات کنترلی پیچیده رو بندازن رو دوش زبان گفتگو که براحتی بشه سیستم های پیچیده ای رو فقط با چند تا جمله کنترل کرد! 

منطق پایه

بیاید یه نگاه دوباره به منطق بولی بندازیم؛

سه تا اپراتور ابتدایی “و” ، “یا” و “نه” داشتیم که از ترکیبشون عملگرهای دیگه رو میساختیم:

a. NOT 0 = 1

b. 0 AND 1 = 0

c. 1 OR 0 = 1

الف. کاری که این عملگرها انجام میدادن این بود:

NOT A = 1 – A                 ex. NOT 0 = 1 – 0 = 1

A AND B = Min (A , B)      ex. 0 AND 1 = Min(0,1) = 0

A OR B = Max (A , B)       ex. 1 OR 0 = Max(1,0) = 1

ب. ‘AND’  و ‘OR’ یه فرمول ساده دیگه هم داشتن :

A AND B = A x B                   ex. 0 AND 1 = 0 x 1 = 0

A OR B = 1 – (1-A) x (1-B)     ex. 1 OR 0 = 1 – (1-1) x (1-0) = 1

حالا همین داستان رو برای اعداد اعشاری پیاده کنیم:

ex. NOT 0.2 = 1 – 0.2 = 0.8

ex. 0.3 AND 0.7 = 0.3 x 0.7 = 0.21                         Min (0.3 , 0.7) = 0.3

ex. 0.3 OR 0.7 = 1 – (1 – 0.3) x (1 – 0.7) = 0.79       Max (0.3 , 0.7) = 0.7

نمونه ای برای درک بهتر منطق و کنترل فازی

یه مثال ساده از یه خودرو دنده اتومات

اگر سرعت خودرو 100 بود (1) پا رو از پدال گاز بردار (0)

اگر سرعت خودرو صفر بود (0) پدال رو تا آخر فشار بده (1)

این جمله ها بیانگر یه NOT منطقی هستن به این شکل:

P = NOT (S)

پدال گاز = NOT سرعت

حالا اگر سرعت خودرو نزدیک به 100 بود وضعیت پدال چی میشه؟ مثلا سرعت 80 ( طبق تعریفی که اول داشتیم سرعت خودرو همچنان 1 هست اما به اندازه 0.8 )

خب باز هم از همین NOT استفاده میکنیم:

NOT 0.8 = 1 – 0.8 = 0.2

یعنی پدال گاز رو باید فشار بدیم (1) اما به اندازه 0.2

حالا که میخوایم از حالت 0 و 1 بیرون بیایم جمله ها به این صورت تغییر میکنن:

اگر سرعت خودرو بالا بود پدال گاز رو کم فشار بده

اگر سرعت خودرو پایین بود پدال گاز رو زیاد فشار بده

این دوتا جمله ناخواسته یه جمله سوم برامون میسازن:

NOT 0.5 = 1 – 0.5 = 0.5

یعنی اگر سرعت خودرو متوسط بود پدال گاز رو وسط نگه دار.

اما معیار کلمات بالا، زیاد، کم، گرم، سرد، پایین و … چیه؟ وقتی میگیم سرعت بالا یعنی دقیقا چقدر؟

ما این مقادیر 0.8 ، 0.5 ، 0.7 و … رو از کجا پیدا کردیم؟

Fuzzification یا فازی سازی

مقدار این کلمات در تابعی به نام تابع عضویت در یک مجموعه فازی مشخص میشن که میتونن یه تابع ذوزنقه ای یا مثلثی یا حتی تک نقطه ای یا اگر بخواد کار یه خورده حرفه ای تر باشه تابع زیگموید یا همون S type باشن که ما خودمون باید اونها رو بسته به عملکرد سیستم مورد نظر تعریف کنیم.

این تابع برای سرعت خودرو میتونه به این شکل باشه :

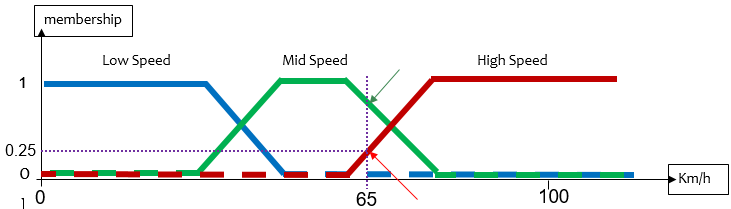
تعریفی که اول بحث داشتیم اینجا میتونه واضح تر باشه، به فلش قرمز رنگ دقت کنید، سرعت 65 کیلومتر بر ساعت همچنان میتونه عضوی از سرعتهای بالا هم به حساب بیاد اما با درجه عضویت 0.25 و عضو سرعتهای متوسط هم هست با درجه عضویت 0.75 (فلش سبز).

مقدار پتانسیومتر پدال گاز که خروجی سیستم هست هم میتونیم به همین شکل تعریف کنیم و مقادیر بدست آمده از توابع ورودی رو به خروجی منتقل کنیم:

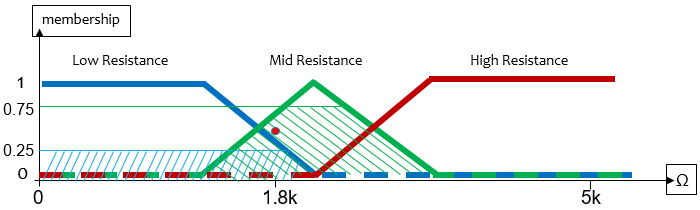
Defuzzification یا فازی زدایی

مرحله آخر کار بدست آوردن مقدار واقعی و دقیق پتانسیومتر پدال گازه و روش عمومی این کار تعیین مرکز ثقل نواحی مشترک هست که در تصویر کاملا روشنه.

اگر بخوایم سرعت رو 65 بمونه پدال باید 0.25 عضو مجموعه کم و 0.75 عضو متوسط باشه. سطح زیر منحنی ها رو با هم OR میکنیم و مقدار x نقطه ثقلش رو به عنوان خروجی استفاده میکنیم. برای مثال ما پتانسیومتر پدال باید روی 1.8KΩ باشه.

تابع عضویت باید برای هر متغیری که در یک سیستم کنترل نقش داره تعریف بشه چه ورودی چه خروجی. ضمن اینکه هرچقدر این توابع بهتر و دقیق تر مشخص بشن به کم شدن نوسان خروجی سیستم کمک میکنه.

برتری های منطق و کنترل فازی

• مهمترین و اصلی ترین و اساسی ترین ویژگی فازی، توانایی چند متغیره (چند ورودی و چند خروجی MIMO) بودنشه که این روش رو واقعا ارزشمند میکنه و کل معایبش رو میبره تو سایه!. بیشتر سیستم هایی که در دنیای پیرامون ما هستند چند متغیره اند که با توجه به ارزش دقت نهایی و میزان پیچیدگی کنترل، اونها رو به بلاکهای تک ورودی تک خروجی (SISO) تقسیم میکنن. همین کار سبب از بین رفتن بخشی از اثرات از عاقبت سیستم میشه وگرنه باید بشینیم کلی معادله حالت و ژاکوبین و … بنویسیم. توی همین مثال خودرو، بجز وضعیت پدال گاز، وضعیت پدال ترمز و دریچه گاز و گیربکس و سنسورهای مختلف و … در سرعت تاثیر دارن. قطعا هیچ مهندسی برای یه سیستم یک ورودی بازای یک خروجی PID رو ول نمیکنه بره سراغ فازی.

• ساده بودن فهم و طراحی یه سیستم فازی ( اگر اصولش رو خوب یاد گرفته باشید ) از هر سیستم کنترل دیگه ای ساده تره بغیر از ON-OFF البته.

• الفت با متغیرهای زبانی ؛ چی بهتر از اینکه شما حرف بزنید و یه سیستم بگه به روی چشم!!

• انعطاف؛ در این نوع کنترل، خطی یا غیرخطی بودن سیستم معنای ریاضی نداره!

• …

معایب کنترل فازی

• بزرگترین عیب کنترل فازی اینه که نمیشه نگاه ریاضی و سیستماتیک بهش داشت، مثلا تحلیلش کنیم و قطبها و نقاط ناپایداریشو دربیاریم، کاری که تو سیستمهای کنترل کلاسیک کاملا مرسومه. 

• مشکل بعدی نوسان ذاتی خروجیهاست که یکی از دلایلش شکل تعریف توابع عضویت هست. برای همین کنترل فازی تو سیستم هایی که لَخت هستن بهتر جواب میده. ( اگرچه این مشکل به روشهایی قابل حله، مثلا ترکیب فازی و PID )

• …

کاربردهای کنترل فازی

• تقریبا تمام خودروها و وسایل نقلیه امروزی؛ از کنترل مصرف سوخت تا ترمز
• عملکرد ایمن و بهینه موتورهای دیزل
• کنترل شرایط محیطی ، تهویه مطبوع ، یخچال بدون برفک ، …
• هوش مصنوعی
• پیش بینی وضعیت هوا
• تشخیص الگو
• فیلترینگ فضای مجازی
• مدل کردن سیستم های اقتصادی برای پیشبینی وضعیت آینده اون سیستم  

موفق باشید